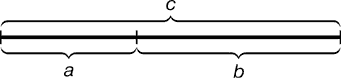Золотое сечение. Золотой треугольник: различия между версиями
(→Определение Золотого сечения) |
(→Золотые треугольники) |
||
| Строка 48: | Строка 48: | ||
Рассмотрим золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618. В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками. | Рассмотрим золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618. В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками. | ||
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой. | Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой. | ||
| + | |||
| + | [[Файл:Петров Артем золотое сечение3.gif]] | ||
Для построения пентаграммы необходимо построить правильный пятиугольник. | Для построения пентаграммы необходимо построить правильный пятиугольник. | ||
Версия 16:19, 9 апреля 2014
Содержание
Введение
Человек различает окружающие его предметы по цвету, вкусу, запаху, форме. Интерес к форме какого-либо предмета может быть вызван жизненной необходимостью, а может быть и красотой формы. Форма, в основе построения которой лежит принцип “золотого сечения”, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Классическими проявлениями золотого сечения являются предметы обихода, скульптура и архитектура, математика, музыка и эстетика. В предыдущем столетии с расширением области знаний человечества резко увеличилось количество сфер, где наблюдается феномен золотой пропорции. Это биология и зоология, экономика, психология, кибернетика, теория сложных систем, и даже геология и астрономия. Ежегодно издаются несколько книг, посвященных этой проблеме, постоянно расширяя область приложения золотого сечения. Авторы этих исследований связывают золотое сечение с такими несовместимыми, на первый взгляд понятиями, как красота, асимметрия, рекурсия, самоорганизация и пропорция. За последние годы появились интересные интернет-сайты, посвященные золотому сечению.
Цели и задачи:
Цель работы: изучить золотое сечение и золотые треугольники.
Задачи работы:
1.Изучить понятие о золотом сечении
2. Узнать о золотых треугольниках
3. Найти золотое сечение в выбранном фото и картине.
Определение Золотого сечения
Как известно, «золотая» пропорция создаёт зрительное ощущение гармонии и равновесия. Но помимо эстетических воздействий она обладает ещё интересными математическими свойствами. Существует бесконечное множество разбиений отрезка на две части. И лишь единственный способ разбиения такой, что отношение всего отрезка к его большей части равно отношению большей части к его меньшей части, т.е. с : b = b : а
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление величины (например, длины отрезка) на две части таким образом, при котором отношение большей части к меньшей равно отношению всей величины к её большей части. Или, если использовать вычисленную величину золотого сечения, — это деление величины на две части — 62 % и 38 % (процентные значения округлены). Число называется также золотым числом. Приблизительная величина золотого сечения равна 1,6180339887. Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
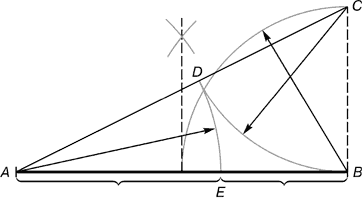
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется отрезком с точкой А. На отрезке AC от точки С откладывается отрезок, равный ВС, заканчивающийся точкой D. На отрезке AB от точки А откладываем отрезок АЕ, равный отрезку AD. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
История Золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле также заложены пропорции золотого деления. В дошедшей до нас античной литературе золотое деление впервые упоминается в “Началах” Евклида. Во 2-й книге “Начал” дается геометрическое построение золотого деления. В средневековой Европе с золотым делением познакомились по арабским переводам “Начал” Евклида. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи. «Пусть никто не будучи математиком, не посмеет читать мои труды.». Он, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась “О перспективе в живописи”. Его считают творцом начертательной геометрии.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя “Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности”.
Золотые треугольники
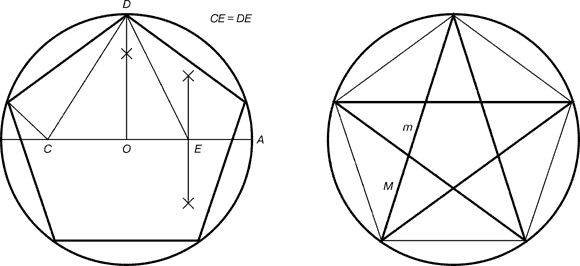
Существуют золотые прямоугольники треугольники пятиугольники и спирали. Рассмотрим золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618. В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками. Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
Для построения пентаграммы необходимо построить правильный пятиугольник. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения золотого прямоугольника.
Золотое сечение в архитектуре и живописи
Рассмотрим строения города Сургута. Во многих постройках присутствует золотое сечение, однако золотой треугольник не так часто встречается в архитектуре города. На фото представлена церковь Всех Святых. На этой фотографии соблюдаются пропорции золотого треугольника.
Медведева Олеся Анатольевна – югорская художница. Она живет и работает в городе Нижневартовск. Является участницей городских, областных, окружных, зональных, всероссийских, международных выставок. Одна из её картин показывает, что золотые треугольники встречаются также и в живописи.
Заключение
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Природа, понимаемая как весь мир в многообразии его форм, состоит как бы из двух частей: живая и неживая природа. Для творений неживой природы характерна высокая устойчивость, слабая изменчивость, если судить в масштабах человеческой жизни. Мир неживой природы - это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир природы - это прежде всего мир гармонии, в которой действует "закон золотого сечения". Повсюду мы встречаем золотое сечение, но лишь обратив на него свое пристальное внимание, мы сможем увидеть истинную красоту.
Список литературы
1. Азевич А.И. От золотой пропорции к ее "производным". // Квант – 1995. - № 3. – С. 55.
2. Хинн О.Г. под общ. Ред. ООО «Издательство АСТ-ЛТД» 2004 г. «Я познаю мир: математика».
3. Васютинский Н.А. Золотая пропорция. – М.: Молодая гвардия, 1990.
4. Виленкин Н.Я. и др. За страницами учебника математики, 10-11. – М.: Просвещение, 1996.
5. Волошинов А.В. Математика и искусство. – М.: Просвещение, 1992.
6. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов. – М.: Мнемозина, 2005