Золотое сечение в архитектуре города Санкт-Петербурга: различия между версиями
(→Золотое сечение в архитектуре города Санкт-Петербурга) |
|||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 4: | Строка 4: | ||
Цель: Доказать, что в архитектурных объектах присутствуют пропорции золотого сечения | Цель: Доказать, что в архитектурных объектах присутствуют пропорции золотого сечения | ||
Задачи: | Задачи: | ||
| + | |||
• Изучить понятие «золотое сечение» и его историю. | • Изучить понятие «золотое сечение» и его историю. | ||
| Строка 105: | Строка 106: | ||
o http://worldwalk.info/ru/catalog/262/ | o http://worldwalk.info/ru/catalog/262/ | ||
| + | |||
| + | ==Дополнительные ресурсы== | ||
| + | |||
| + | [[Файл:Золотое сечение. Деменковец Анастасия.pdf]] | ||
Текущая версия на 10:57, 15 апреля 2014
Содержание
Введение
При изучении темы «Подобные треугольники» я познакомилась с такими понятиями как «пропорциональные отрезки». Оказывается, что пропорциональное деление отрезка при определенном отношении, является ничем иным как золотым сечением. Я решила углубиться в эту тему и выбрала золотое сечение в архитектуре.
Цель: Доказать, что в архитектурных объектах присутствуют пропорции золотого сечения Задачи:
• Изучить понятие «золотое сечение» и его историю.
• Изучить понятие «золотой прямоугольник».
• Рассмотреть золотое сечение в архитектуре.
• Рассмотреть архитектурные объекты города Санкт-Петербурга с позиции пропорций золотого сечения
• Подвести итоги
Гипотеза: Я предполагаю, что в архитектуре Санкт-Петербурга преобладает фигура золотой прямоугольник.
Актуальность: Мы путешествуем по разным странам и городам, видим памятники, величественные скульптуры и архитектурные объекты. Почему бы не узнать о тонкостях и особенностях их строения?
Золотое сечение и его история
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему. Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Золотое сечение (отношение) — иррациональное число, приблизительно равное 1.6180339887
С математической точки зрения, отношение большей части к меньшей в золотом сечении выражается квадратичной иррациональностью
![]()
и, наоборот, отношение меньшей части к большей
Число ф (фи) называется также золотым числом.
Золотой прямоугольник
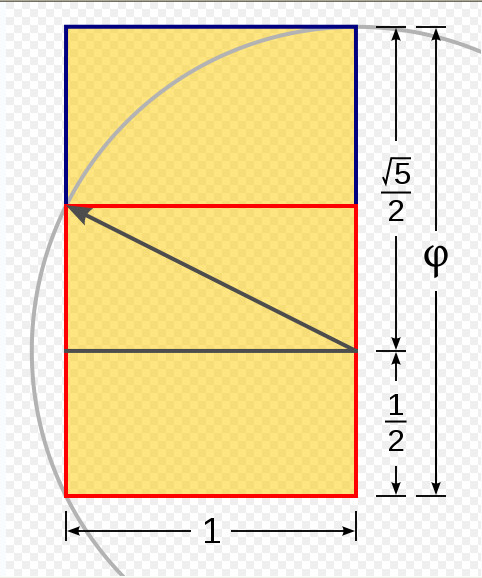
Золотой прямоугольник является одной из золотых фигур. Чтобы его построить, нужно сделать следующее. Построим квадрат ABCD со стороной AB. Нам нужно разбить квадрат на два равных прямоугольника. Для этого разделим отрезки AB и CD на две равные части, а точки, которые являются серединами каждого отрезка, соединим. В одном из прямоугольников проведем диагональ. Возьмем циркуль и проведем окружность радиусом данной диагонали до пересечения с продолжением стороны квадрата. Закончим построение прямоугольника. Таким образом, все его стороны пропорциональны.
Золотое сечение в античной архитектуре
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании. (Площадь основания пирамиды относится к площади всех 4 боковых граней) Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению.
Золотое сечение в архитектуре города Санкт-Петербурга
Архитекту́ра Санкт-Петербу́рга, в особенности его исторического центра, представляет собой созданный в XVIII—XX веках один из самых выдающихся по выразительности архитектурных столичных комплексов. На территории России Санкт-Петербург стал первым крупным современным городом, на территории Европы — самой молодой столицей. Особенностями архитектуры Санкт-Петербурга являются продуманная регулярность застройки, соразмерность городских ансамблей, учёт влияния неброской природной среды, гармоничная полифония различных архитектурных стилей. Для работы с пропорциями золотого сечения я выбрала следующие архитектурные объекты: • Казанский собор • Исаакиевский собор • Базилика святой Екатерины Александрийской
1. Казанский собор
Каза́нский кафедра́льный собо́р (Собор Казанской иконы Божией Матери) — один из крупнейших храмов Санкт-Петербурга, выполненный в стиле ампир. Длина главного корпуса собора с запада на восток составляет 72,5 метра; трансепт немногим короче — 56,7 метра. Вершина купола поднята на высоту 62 метров. Размах наружной колоннады превышает 100 метров, а высота каждой из 92 колонн, составляющих ее, почти 13 метров. Своды, перекрывающие проезды боковых портиков колоннады, переброшены от одной опоры до другой на расстояние 7,8 метра. В главном входе собора я заметила поразительное сходство в размещении колонн Казанского собора и Храма Парфенона. По расчетам мне удалось выполнить построения. Таким образом, в главном входе собора присутствуют пропорции золотого сечения. Так как цель и основная идея моей работы заключается в определении пропорций золотого прямоугольника в архитектурных сооружениях, я решила построить этот прямоугольник. Я обнаружила, что линии и стороны соответствуют какому-либо выступу или барельефу на здании. Линии так же разделили главный вход на пропорциональные отрезки. Я определила это, исходя из построений, сделанных мной ранее.
2. Исаакиевский собор
Исаа́киевский собо́р (официальное название - собор преподобного Исаакия Далматского) — крупнейший православный храм Санкт-Петербурга. Он явился одним из крупнейших в мире купольных зданий (диаметр купола – 21,8 м). Высота Исаакиевского собора – 101,5 м, размеры в плане (с портиками) 111,5 на 97,6 м.
Аналогично своей предыдущей работе с Казанским кафедральным собором, я рассмотрела и Исаакиевский собор. Колонны главного входа так же образуют пропорции золотого сечения. Я выполнила построения. Следуя построениям золотого прямоугольника, я разделила выбранную мной часть на пропорциональные отрезки. И снова я обнаружила, что линии соответствуют выступам и барельефам. Вновь замечаю, что линии прямоугольника делят вход на пропорциональные отрезки. Их соотношение соответствует реальным размерам собора.
3. Базилика святой Екатерины Александрийской
Базилика святой Екатерины Александрийской — католический храм в Санкт-Петербурге, один из старейших католических храмов России. Памятник архитектуры. Здание имеет форму латинского креста, с поперечным трансептом, увенчано большим куполом. Длина здания храма — 44 метра, ширина — 25 метров, высота — 42 метра.
Работа с базиликой и мои подсчеты подобны сделанному с предыдущими двумя зданиями. Выполнив необходимые расчеты и построения, я снова заметила, что линии соответствуют выступам, изгибам и барельефам на здании. Пропорциональное деление фасада так же присутствует.
Золотое сечение в картине
Портрет Петра I
Чтобы закрепить полученные знания и приобретенный опыт в построениях, я разделила Портрет Петра I соответственно пропорциям золотого сечения.
Заключение
Я работала с большим количеством информации и сумела выделить все самое основное. Работать с этой темой мне было очень интересно. Я узнала о золотом сечении, о его античных корнях и чертах в архитектуре. Зная, как строится золотой прямоугольник, зная размеры архитектурных объектов, мне удалось построить прямоугольник, следуя пропорции. На этих чертежах я доказала, что в архитектурных объектах преобладает фигура золотого прямоугольника. У меня получилось применить знания о золотом сечении и разделить картину «Портрет Петра I» на пропорциональные отрезки.
Информационные ресурсы
o http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
o http://ru.wikipedia.org/wiki
o http://ru.science.wikia.com/wiki/Золотое_сечение
o http://arx.novosibdom.ru/node/419
o http://worldwalk.info/ru/catalog/262/