Участник:Эмин: различия между версиями
Эмин (обсуждение | вклад) |
Эмин (обсуждение | вклад) |
||
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 34: | Строка 34: | ||
* [[Метод Монте-Карло]] (метод статистических испытаний); | * [[Метод Монте-Карло]] (метод статистических испытаний); | ||
* Метод имитационного моделирования[[(статистическое моделирование)]]. | * Метод имитационного моделирования[[(статистическое моделирование)]]. | ||
| + | |||
| + | {| border 1 | ||
| + | | Ячейка 1, строка 1 | ||
| + | | Ячейка 2, строка 1 | ||
| + | |- | ||
| + | | Ячейка 1, строка 2 | ||
| + | | Ячейка 2, строка 2 | ||
| + | |} | ||
| Строка 79: | Строка 87: | ||
*Scilab | *Scilab | ||
*Maxima | *Maxima | ||
| + | |||
| + | |||
| + | == См. также == | ||
| + | |||
| + | *Сети Петри | ||
| + | *[[Сетевое моделирование]] | ||
| + | |||
| + | |||
| + | |||
| + | == Примечания == | ||
| + | |||
| + | 1.↑ Муха В. С. Вычислительные методы и компьютерная алгебра: учеб.-метод. пособие. — 2-е изд., испр. и доп. — Минск: БГУИР, 2010.- 148 с.: ил, ISBN 978-985-488-522-3, УДК 519.6 (075.8), ББК 22.19я73, М92 | ||
| + | |||
| + | |||
| + | == Литература == | ||
| + | |||
| + | *Хемди А. Таха Глава 18. Имитационное моделирование // Введение в исследование операций = Operations Research: An Introduction. — 7-е изд. — М.: «Вильямс», 2007. — С. 697-737. — ISBN 0-13-032374-8 | ||
| + | |||
| + | *Строгалев В. П., Толкачева И. О. Имитационное моделирование. — МГТУ им. Баумана, 2008. — С. 697-737. — ISBN 978-5-7038-3021-5 | ||
| + | |||
| + | |||
| + | |||
| + | == Ссылки == | ||
| + | |||
| + | *Компьютерное и статическое имитационное моделирование на Интуит.ру | ||
| + | *Национальное общество имитационного моделирования | ||
| + | *Имитационное моделирование в задачах технологического инжиниринга Макаров В. М., Лукина С. В., Лебедь П. А. | ||
| + | |||
| + | Это заготовка статьи по математике. Вы можете помочь проекту, исправив и дополнив её. | ||
| + | Категории: | ||
| + | |||
| + | Математическое моделирование | ||
| + | Программы математического моделирования | ||
Текущая версия на 12:03, 6 марта 2013
Содержание
Имитационное моделирование
Имитационное моделирование (ситуационное моделирование) — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.
Имитационное моделирование — это метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную систему, с которой проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте).
Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае аналитическая модель заменяется имитатором или имитационной моделью.
Имитационным моделированием иногда называют получение частных численных решений сформулированной задачи на основе аналитических решений или с помощью численных методов[1].
Имитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта.
Применение имитационного моделирования
К имитационному моделированию прибегают, когда:
- дорого или невозможно экспериментировать на реальном объекте;
- невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные;
- необходимо сымитировать поведение системы во времени.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между её элементами или другими словами — разработке симулятора (англ. simulation modeling) исследуемой предметной области для проведения различных экспериментов.
Имитационное моделирование позволяет имитировать поведение системы во времени. Причём плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны или опасны. С наступлением эпохи персональных компьютеров производство сложных и уникальных изделий, как правило, сопровождается компьютерным трёхмерным имитационным моделированием. Эта точная и относительно быстрая технология позволяет накопить все необходимые знания, оборудование и полуфабрикаты для будущего изделия до начала производства[источник не указан 284 дня]. Компьютерное 3D-моделирование теперь не редкость даже для небольших компаний[источник не указан 284 дня].
Имитация как метод решения нетривиальных задач получила начальное развитие в связи с созданием ЭВМ в 1950-х — 1960-х годах.
Можно выделить две разновидности имитации:
- Метод Монте-Карло (метод статистических испытаний);
- Метод имитационного моделирования(статистическое моделирование).
| Ячейка 1, строка 1 | Ячейка 2, строка 1 |
| Ячейка 1, строка 2 | Ячейка 2, строка 2 |
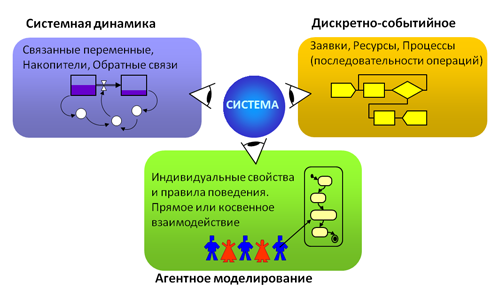
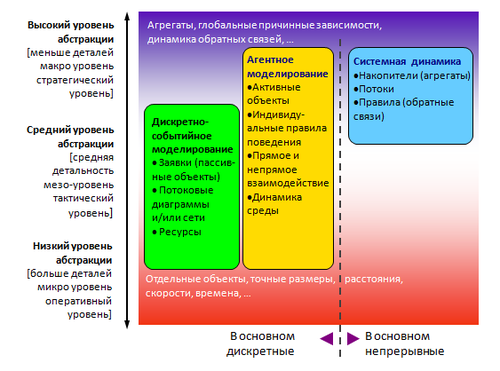
Виды имитационного моделирования
- Агентное моделирование — относительно новое (1990-е-2000-е гг.) направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот, когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей — получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении её отдельных активных объектов и взаимодействии этих объектов в системе. Агент — некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться.
- Дискретно-событийное моделирование — подход к моделированию, предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы, такие, как: «ожидание», «обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений — от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов. Основан Джеффри Гордоном в 1960-х годах.
- Системная динамика — парадигма моделирования, где для исследуемой системы строятся графические диаграммы причинных связей и глобальных влияний одних параметров на другие во времени, а затем созданная на основе этих диаграмм модель имитируется на компьютере. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики строят модели бизнес-процессов, развития города, модели производства, динамики популяции, экологии и развития эпидемии. Метод основан Джеем Форрестером в 1950 годах.
Области применения
- Бизнес-процессы
- Боевые действия
- Динамика населения
- Дорожное движение
- ИТ-инфраструктура
- Математическое моделирование исторических процессов
- Логистика
- Пешеходная динамика
- Производство
- Рынок и конкуренция
- Сервисные центры
- Цепочки поставок
- Уличное движение
- Управление проектами
- Экономика здравоохранения
- Экосистема
- Информационная безопасность
Свободные системы имитационного моделирования
- Scilab
- Maxima
См. также
- Сети Петри
- Сетевое моделирование
Примечания
1.↑ Муха В. С. Вычислительные методы и компьютерная алгебра: учеб.-метод. пособие. — 2-е изд., испр. и доп. — Минск: БГУИР, 2010.- 148 с.: ил, ISBN 978-985-488-522-3, УДК 519.6 (075.8), ББК 22.19я73, М92
Литература
- Хемди А. Таха Глава 18. Имитационное моделирование // Введение в исследование операций = Operations Research: An Introduction. — 7-е изд. — М.: «Вильямс», 2007. — С. 697-737. — ISBN 0-13-032374-8
- Строгалев В. П., Толкачева И. О. Имитационное моделирование. — МГТУ им. Баумана, 2008. — С. 697-737. — ISBN 978-5-7038-3021-5
Ссылки
- Компьютерное и статическое имитационное моделирование на Интуит.ру
- Национальное общество имитационного моделирования
- Имитационное моделирование в задачах технологического инжиниринга Макаров В. М., Лукина С. В., Лебедь П. А.
Это заготовка статьи по математике. Вы можете помочь проекту, исправив и дополнив её.
Категории:
Математическое моделирование Программы математического моделирования